Mamy dane na podstawie których należy wyznaczyć prostą, która będzie przechodziła możliwie najbliżej wszystkich punktów doświadczalnych
| index | x | y |
| 1 | 2 | 2.5 |
| 2 | 4 | 10 |
| 3 | 6 | 32 |
| 4 | 8 | 40 |
| 5 | 10 | 60 |
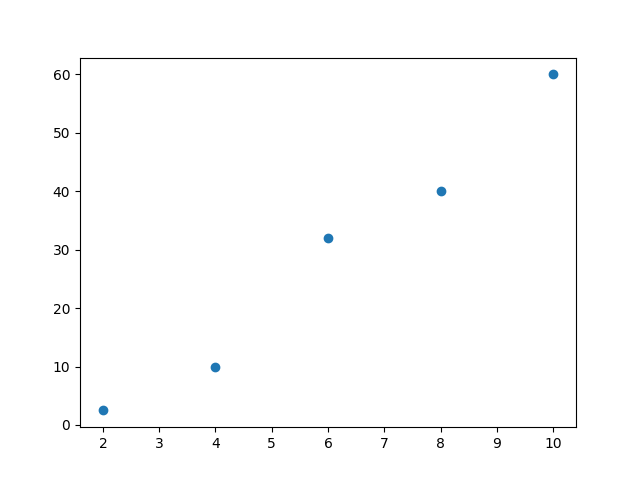
Równanie prostej ma postać y = ax+b
Wzór:
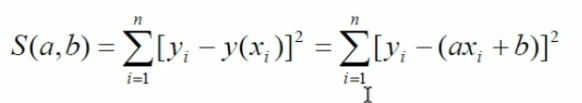
S(a,b)=[2.5-(2a+b)]²+ [10-(4a+b)]² + [32-(6a+b)]² + [40-(8a+b)]² + [60-(10a+b)]²
Następnie szukamy minimum funkcji za pomocą pochodnych cząstkowych i warunku istnienia ekstremum. Otrzymujemy:
2[2.5-2a-b)](-2)+2[10-4a-b)](-4) + 2[32-6a-b)](-6) + 2[40-8a-b)](-8) + 2[60-10a-b)](-10) = 0
oraz:
2[2.5-2a-b)](-1)+2[10-4a-b)](-1) + 2[32-6a-b)](-1) + 2[40-8a-b)](-1) + 2[60-10a-b)](-1) = 0
Po uproszczeniu:
440a + 60b = 2314
60a +10b = 289
Rozwiązanie układu równań:
a = 7.25
b = – 14.6
Na wykresie przedstawiono linię prostą określoną przez równanie y = 7.25 * x – 14.6:
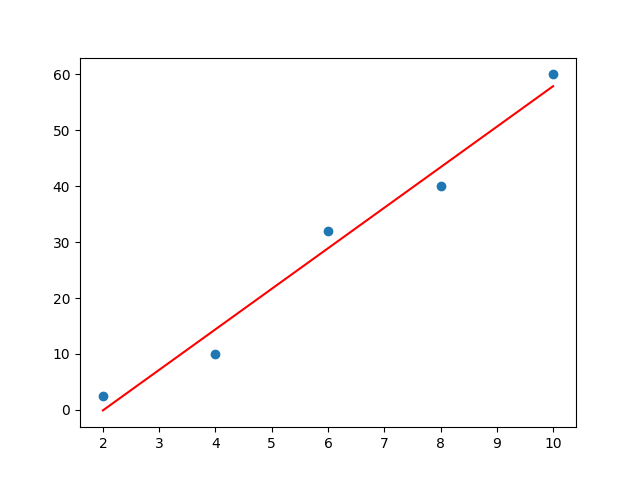
Przykładowe rozwiązanie w Python:
# -*- coding: utf-8 -*-
# Regresja liniowa:
import numpy as np
import matplotlib.pyplot as plt
import sklearn.linear_model as slm
X = np.array([[1], [2.3], [4.1], [6.12], [8], [10.3]])
Y = np.array([0.1, 0.25, 0.39, 0.59, 0.8, 1.01])
# Tworzymy obiekt klasy LinearRegression:
regresja = slm.LinearRegression()
regresja.fit(X,Y)
print('Wyraz wolny jest równy: %s' % round(regresja.intercept_,3))
print('Współczynnik kierunkowy wynosi: %s' % np.round(regresja.coef_,3))
print('Współczynnik dopasowania wynosi: %s' % round(regresja.score(X,Y),3))
P = np.array([0.098*x + 0.006 for x in np.linspace(1,11,50)])
plt.figure()
plt.scatter(X, Y, c='r', s=1.5)
plt.plot(np.linspace(1,11,50), P)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Zebrane dane')
plt.show()