Wyznacznik macierzy (det A) możemy zastosować wyłącznie dla macierzy kwadratowych.
Jeżeli macierz ma stopień n = 1 (A = [a11]), to det A = a11
Jeżeli A ma stopień n > 1, to :
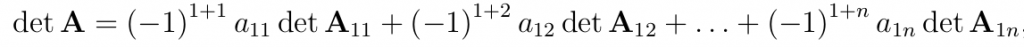
Dla macierzy stopnia n=2 wyznacznik liczymy w następujący sposób:
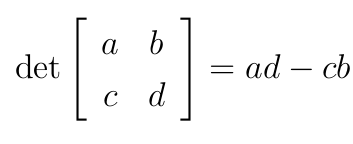
Dla macierzy stopnia n=3 wyznacznik liczymy stosując tzw. metodę Sarrusa:
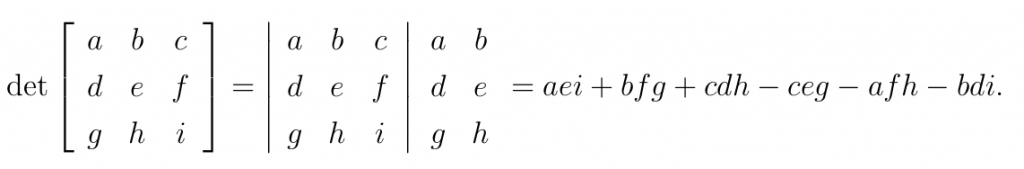
Dopełnienie algebraiczne:

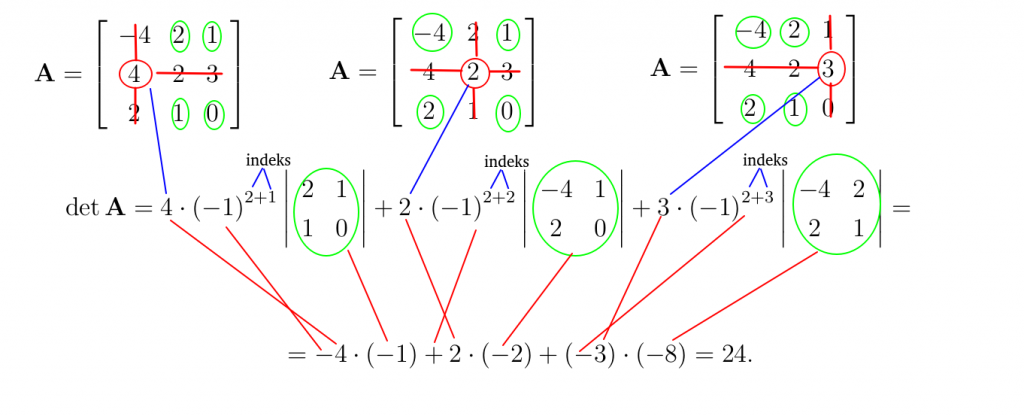
Poniżej obliczam wyznacznik macierzy (det A) rozwinięciem Laplace’a względem 2− ego wiersza:
Poniżej przykład obliczenia wyznacznika macierzy za pomocą Python/ Numpy.
import numpy
M = [[-4, 2, 1], [4, 2, 3], [2, 1, 0]]
print(numpy.linalg.det(M))Podstawowe własności wyznaczników:
Wyznacznik macierzy trójkątnej górnej i dolnej równy jest iloczynowi wyrazów na głównej przekątnej.
Wyznacznik macierzy kwadratowej mającej kolumnę albo wiersz złożone z samych zer jest równy zero.
Wyznacznik macierzy mającej dwie identyczne kolumny albo dwa identyczne wiersze jest równy zero.
Wyznaczniki macierzy danej i transponowanej są równe.
Jeżeli w macierzy kwadratowej przestawimy między sobą dwie kolumny albo dwa wiersze, to wyznacznik zmieni znak na przeciwny.
Jeżeli wszystkie wyrazy kolumny lub wiersza w danej macierzy kwadratowej mają wspólnych czynnik, to czynniki ten możemy wyłączyć przed znak wyznacznika.
Wyznacznik macierzy nie zmieni się, jeżeli do elementów dowolnej kolumny [wiersza] dodamy odpowiadające im wyrazy innej kolumny [wiersza] pomnożone przez dowolną
liczbę.
