
∀ – dla każdego
∃ – istnieje
Elementem neutralnym dla dodawania jest 0, a dla mnożenia jest 1.
Elementem odwrotnym w dodawaniu dla 1 jest minus 1.
1 – 1(element odwrotny) = 0(element neutralny)
Przykład. Sprawdźmy czy poniższe działanie jest grupą:
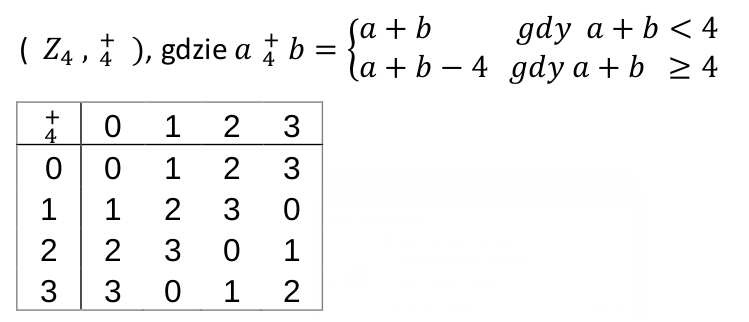
- Działanie jest działaniem wewnętrznym ponieważ każdy z elementów (0, 1, 2, 3) zawarty jest w zbiorze.
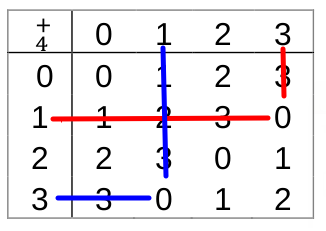
- Zachodzi łączność. Poniżej przykładowe porównanie(1+3 = 3+1)
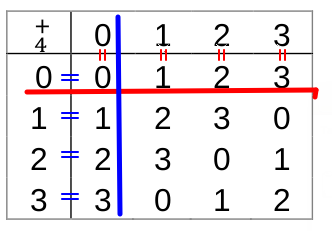
3. Istnieje element neutralny, e=0. Poniżej sprawdzamy, czy gdy 0 zadziała na dowolny element to otrzymamy identyczny element.
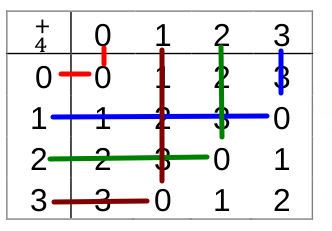
4. Istnieje element przeciwny dla każdego elementu. Poniżej sprawdzamy które elementy są przeciwne dla każdego elementu (czyli takie, które po zadziałaniu dadzą element neutralny, którym w tym przypadku jest 0).
Odpowiedź: Powyższe działanie jest grupą. Dodatkowo jest grupą abelową, ponieważ dodawanie jest przemienne, czyli nie musimy przejmować się kolejnością wykonywania działania.
