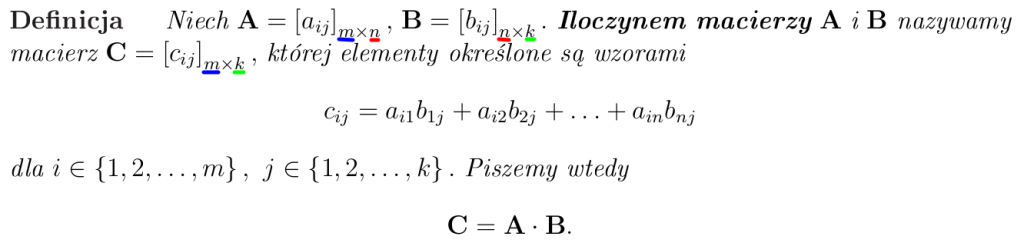
Z defnicji wynika, że iloczyn A · B jest wykonalny gdy ilość kolumn macierzy A jest taka sama jak ilość wierszy macierzy B. Otrzymana macierz ma tyle wierszy ile miała macierz A i tyle kolumn ile miała macierz B. Mnożenie macierzy polega zatem na mnożeniu kolejnych wierszy pierwszej macierzy przez kolejne kolumny drugiej macierzy (przez mnożenie rozumiemy iloczyn skalarny).

Uwaga. Mnożenie macierzy nie jest na ogół przemienne.

Własności działań na macierzach:

Jeśli macierz A ma wymiar m × n oraz macierze B i C wymiar n × k, to
A (B + C) = AB + AC.

Jeśli macierze A i B mają wymiar m × n oraz macierz C wymiar n × k, to
(A + B) C = AC + BC.

Jeśli macierz A ma wymiar m × n, macierz B wymiar n × k oraz α jest liczba
rzeczywistą, to
A (αB) = (αA) B = α (AB) .

Jeśli macierz A ma wymiar m × n , macierz B wymiar n × k oraz macierz C wymiar k × l, to
(AB) C = A (BC) .

Jeśli macierz A ma wymiar m × n, to
AI n = I m A = A.

Poniżej przykłady mnożenia macierzy z wykorzystaniem Python.

import numpy as np

ai = int(input("Określ liczbę wierszy dla macierzy A :\n"))
aj = int(input("Określ liczbę kolumn dla macierzy A :\n"))
bi = int(input("Określ liczbę wierszy dla macierzy B : \n"))
bj = int(input("Określ liczbę kolumn dla macierzy B : \n"))

if aj != bi:
    print("iloczyn A·B niemozliwy, poniewaz ilosc kolumn macierzy A jest inna niz ilosc wierszy macierzy B")
    pass

else:
    A = np.array(np.random.rand(ai, aj))
    B = np.array(np.random.rand(bi, bj))
    C = np.zeros((ai, bj))

    for i in range(len(A)):
       for j in range(len(B[0])):
           for k in range(len(B)):
               C[i][j] += A[i][k] * B[k][j]

    for r in C:
       print(r)


    print('Ponizej algebraiczne mnozenie macierzy za pomoca funkcji dot() / Numpy')
    print(A.dot(B))
    print('Ponizej algebraiczne mnozenie macierzy za pomoca symbolu @')
    print(A @ B)