Regresja logistyczna

Stosowana, gdy mamy do czynienia ze zmiennymi typu dychotomicznego. Przyjmuje dwie wartości, np. 1-tak (zdarzenia pożądane) / 2-nie.

Model regresji logistycznej oparty jest o funkcję logistyczną postaci:

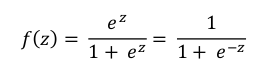
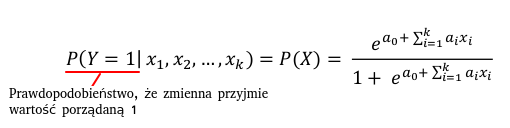
Funkcja logistyczna przyjmuje wartości od 0 (gdy x dąży do minus nieskończoności) do 1 (gdy x zmierza do plus nieskończoności):

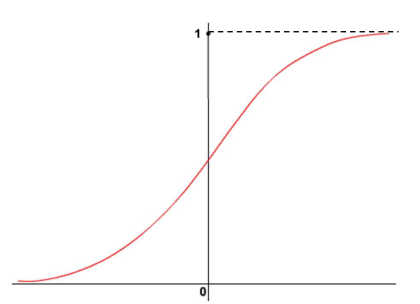
Warunkiem zastosowania regresji logistycznej jest odpowiednio duża próba, co w tym przypadku oznacza, że liczność próby n:

n > 10 (k + 1), gdzie k jest liczbą parametrów.

Iloraz szans

W regresji logistycznej, oprócz współczynników regresji i ich statystycznej istotności, dochodzi jeszcze dodatkowy parametr: iloraz szans (odds ratio) dany wzorem:

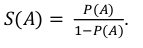
W przypadku, gdy mamy dwie cechy jakościowe, stosujemy podwójną klasyfikację

Pierwsza klasyfikacja może być przykładowo postaci:

• Narażeni i nienarażeni,
• Palący i niepalący,
• Leczeni metodą A i metodą B,
• Szczepieni i nieszczepieni,
• Itp.

Natomiast druga klasyfikacja jest najczęściej postaci:

• Zachorowali, nie zachorowali
• Przeżyli, zmarli
• Parametr biochemiczny w normie, parametr biochemiczny poniżej/powyżej normy, itd.

Dla dwóch grup porównywanych A i B iloraz szans definiowany jest jako stosunek wystąpienia „szansy” A do „szansy” B:

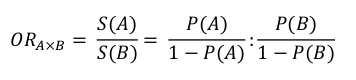
Iloraz szans równy 1 oznacza równoważność ryzyka porównywanych grup. Większy od 1 wskazuje, że szansa wystąpienia danego zdarzenia zdrowotnego w grupie A jest większa niż w grupie B.

Założenia regresji logistycznej

• Losowy dobór próby;
• Odpowiednie kodowanie (model regresji logistycznej wylicza prawdopodobieństwo, że
• zmienna zależna przyjmuje wartość 1);
• Uwzględnienie wszystkich istotnych zmiennych;
• Wyłączenie z modelu wszystkich nieistotnych zmiennych;
• Zależność transformacji logitowej od zmiennych niezależnych jest liniowa;
• Model regresji logistycznej nie wyjaśnia efektów interakcji zmiennych niezależnych;
• Zmienne niezależne nie mogą być współliniowe;
• Regresja logistyczna jest wrażliwa na występowanie punktów odstających. Przed rozpoczęciem analizy należy je usunąć (wykrycie przypadków odstających umożliwia analiza reszt);
• Próba musi być dostatecznie liczna (co najmniej n=100);

Przykład implementacji w Python

from sklearn.linear_model import LogisticRegression

l_clf = LogisticRegression(solver = 'lbfgs')
l_clf.fit(X,Y)
l_prediction = l_clf.predict(test_data)

Przykład na stworzenie i wyświetlenie funkcji:

import matplotlib.pyplot as plt
import math

z = [i for i in range(-10, 11)]


def logistic_regression(lst):
    lst.sort()
    results = []
    for i in lst:
        result = 1 / (1 + math.e ** (- i))
        results.append(result)
    return results


plt.plot(z, logistic_regression(z))
plt.show()